Metrics used in Classification

2018-03-24

We will introduce common metrics used in classification problems: precision, recall, f1, macro_f1, micro_f1, precision-recall curve and ROC curve . Our discussion is based on binary classification problems.

Table of Prediction

Table 1. Prediction table

Based on this table, we will give the definition of precision, recall and f1, f1 is defined as the harmonic mean of precision and recall.

$ precision = \frac{TP}{TP + FP} $

$ recall = \frac{TP}{TP + FN} $

$ f1 = \frac{2}{\frac{1}{precision} \times \frac{1}{precision}} = 2 \times \frac{precision \times recall}{precision + recall}$

precision : among the samples you predict, how many are correctly predict.

recall : among all the postive samples, how many are found by your model.

f1 : a tradeoff for precision and recall for different threshold (we got a probability when predict, if the prob is larger than threshold, we will predict it as postive and vice versa).

Macro and Micro

Macro and micro are different average ways.
Macro f1 treated each class equally, i.e. it doesn’t take each class’ sample num into consideration. Whereas micro f1 take each class’ sample num into consideration, i.e. it computes the weighted average f1 for each class.
Suppose we have $n_0$ samples for class 0, $n_1$ samples for class 1, and $f1_0$ is f1 score for class 0, $f1_1$ is f1 score for class 1. Then

$ macrof1 = \frac{1}{2} \times (f1_0 + f1_1) $

$ microf1 = \frac{n_0 \times f1_0 + n_1 \times f1_1}{n_0 + n_1}$

Confusion Matrix

Confusion matrix is a matrix used to evaluate the accuracy for classification. Each element $C(i, j)$ is the number of samples known to be in group $i$ but predicted to be in group $j$. If $ i == j$ then $C(i, j)$ is the correctly predict num for class $i$. Usually confusion matrix is plotted using a heat map.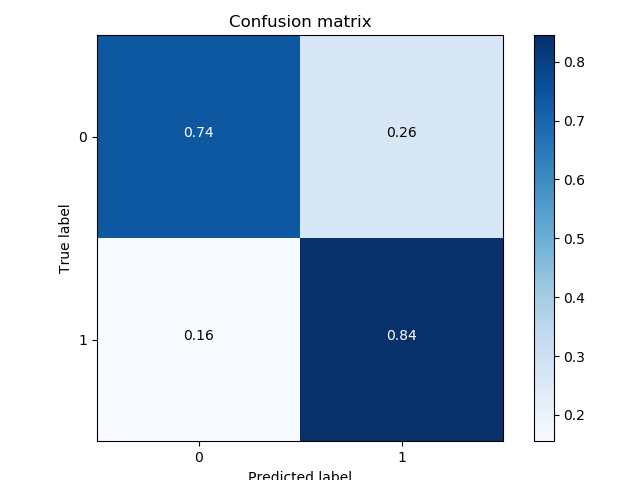
Confusion Matrix

Precision Recall Curve

Precision Recall Curve shows the relationship between recall(x) and precision(y).
It is plotted by adjusting $thereshold$ when predicting labels. Given a trained classifier, we use it to predict some new samples, then we get a list of probabilities, if the probability is larger than $threshold$, we assign it as postive label, else we assign it as negative label. So when we adjust the threshold value, we will get a group of (precision, recall) pairs. Precision Recall Curve is plotted using these pairs.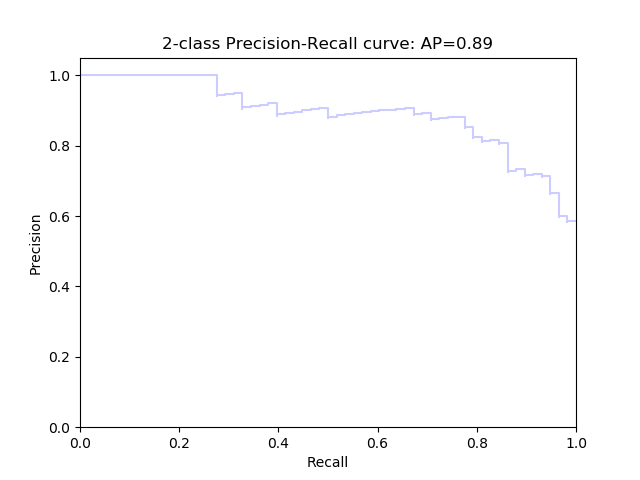
Precision Recall Curve

ROC curve and AUC of ROC

ROC Curve shows the relationship between TPR(x) and FPR(y).

$ TPR = \frac{TP}{TP + FN} $

$ FPR = \frac{FP}{FP + TN} $

Similar to Precision Recall Curve, ROC curve is also plotted by adjusting $thereshold$ when predicting labels.
AUC (area under curve) is the area under the ROC curve.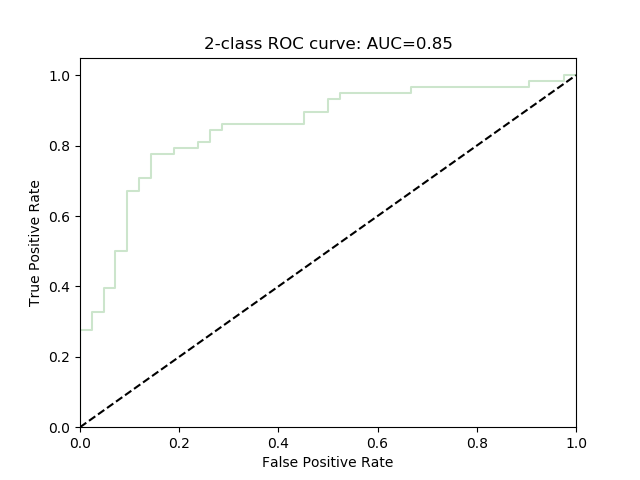
ROC Curve

Trial

Finally, we use sklearn to train a binary classifier and evaluate this classifier using the above metrics.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
"""
Binary classification.
Try scikit learn's classifier with auto generated dataset.
"""
import itertools
import numpy as np
from sklearn import svm
from sklearn.metrics import f1_score, precision_recall_curve, average_precision_score, roc_auc_score, roc_curve, \
    confusion_matrix
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
def make_dataset():
    # generate dataset for binary classification
    X, y = make_classification(n_samples=500, n_classes=2, n_features=4, n_informative=2, flip_y=0.28,
                               weights=[0.4, 0.6], random_state=101)
    # plot dataset
    plt.scatter(X[:, 0], X[:, 1], marker="o", c=y, s=25, edgecolor="k")
    plt.show()
    # split dataset
    train_size = 400
    train_x, train_y = X[:train_size], y[:train_size]
    test_x, test_y = X[train_size:], y[train_size:]
    return train_x, train_y, test_x, test_y
def train(train_x, train_y):
    clf = svm.SVC()
    clf.fit(train_x, train_y)
    return clf
def predict(clf, test_x):
    probs = clf.decision_function(test_x)
    preds = clf.predict(test_x)
    return probs, preds
def macro_average(arr):
    return np.average(arr)
def micro_average(cls_sample_nums, arr):
    return np.dot(cls_sample_nums, arr) / np.sum(cls_sample_nums)
def evaluate(probs, pred_y, true_y):
    # plot precision_recall curve
    avg_precision = average_precision_score(true_y, probs)
    precision, recall, _ = precision_recall_curve(true_y, probs)
    print("Average precision: {:.04f}".format(avg_precision))
    plt.step(recall, precision, color='b', alpha=0.2, where='post')
    plt.xlabel('Recall')
    plt.ylabel('Precision')
    plt.ylim([0.0, 1.05])
    plt.xlim([0.0, 1.0])
    plt.title('2-class Precision-Recall curve: AP={0:0.2f}'.format(avg_precision))
    plt.show()
    # plot roc curve and auc
    fpr, tpr, _ = roc_curve(true_y, probs)
    mAP = roc_auc_score(true_y, probs)
    print("Mean average precision: {:.04f}".format(mAP))
    plt.plot(np.arange(0, 1.1, 0.1), np.arange(0, 1.1, 0.1), "k--")
    plt.step(fpr, tpr, color='g', alpha=0.2, where='post')
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.ylim([0.0, 1.05])
    plt.xlim([0.0, 1.0])
    plt.title('2-class ROC curve: AUC={0:0.2f}'.format(mAP))
    plt.show()
    # plot confusion matrix
    cm = confusion_matrix(true_y, pred_y)
    # normalize cm as the sample num for each class varies
    cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
    plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
    plt.title("Confusion matrix")
    plt.colorbar()
    class_names = ["0", "1"]
    tick_marks = np.arange(len(class_names))
    plt.xticks(tick_marks, class_names)
    plt.yticks(tick_marks, class_names)
    fmt = '.2f'
    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, format(cm[i, j], fmt),
                 horizontalalignment="center",
                 color="white" if cm[i, j] > thresh else "black")
    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')
    plt.show()
    # micro_f1 and macro_f1
    f1_cls0 = f1_score(test_y, pred_y, average="binary", pos_label=0)
    f1_cls1 = f1_score(test_y, pred_y, average="binary", pos_label=1)
    print("f1 for class 0: {:.4f}".format(f1_cls0))
    print("f1 for class 1: {:.4f}".format(f1_cls1))
    cls_sample_nums = np.bincount(test_y)
    # micro_f1 = f1_score(test_y, pred_y, average="micro")
    # macro_f1 = f1_score(test_y, pred_y, average="macro")
    micro_f1 = micro_average(cls_sample_nums, [f1_cls0, f1_cls1])
    macro_f1 = macro_average([f1_cls0, f1_cls1])
    print("Micro f1: {:.4f}".format(micro_f1))
    print("Macro f1: {:.4f}".format(macro_f1))
if __name__ == '__main__':
    train_x, train_y, test_x, test_y = make_dataset()
    clf = train(train_x, train_y)
    pred_probs, pred_y = predict(clf, test_x)
    evaluate(pred_probs, pred_y, test_y)

1
2
3
4
5
6
7
""" console outputs: """
Average precision: 0.8917
Mean average precision: 0.8506
f1 for class 0: 0.7561
f1 for class 1: 0.8305
Micro f1: 0.7993
Macro f1: 0.7933

References:

  1. Scikit Learn
  2. Macro- and micro-averaged evaluation measures